Green’s function retrieval and fluctuations of the cross density of states in multiple scattering me
- de Rosny, J. & Davy, M. in Europhysics Letters
- 3 juin 2014
- 3 min de lecture
A wave propagating in a multiple scattering medium is completely scrambled and generates random intensity patterns. Nevertheless the wave is still correlated in time and space and useful information can be extracted from the cross-correlation of signals recorded at two positions. For an isotropic distribution of sources, the time-derivative of the cross-correlation of a diffuse field measured at two positions is equal to the difference between the causal and anti-causal temporal Green's functions (GF). This has led to the ambient passive imaging method widely used in seismology but which has also been applied to acoustic, elastic and electromagnetic waves. In the frequency domain, the noise cross-correlation function (NCF) reduces to the imaginary part of the GF. When the positions of the probes coincide, the NCF linearly depends on the local density of states (LDOS) which counts the number of modes available at a given position. In optics, the LDOS determines spontaneous and stimulated emission of light. The LDOS exhibits spatial fluctuations caused by scatterers in the vicinity of the source. For two different positions, the NCF gives the cross-density of states (CD0S).
To obtain a good reconstruction of the GF, the noise sources should be evenly distributed in space and the observation time should be long enough. In the other case, a strong deviation from the GF can be observed. Nevertheless it was observed that multiple scattering can help to estimate the Green's functions by minimizing spurious contributions. But a strong contradiction appears in the literature. In the one hand, this conclusion rapidly arose from an analogy with time reversal of waves, since the time-reversal process is a “natural” correlator and it is well known that it is a self-averaging process in regards to the bandwidth of signals. The NCF also tends to be self-averaging in a random medium, even though the noise sources are not equally distributed. In the other hand, when the distance between the emitter and the receiver is larger than one mean free path, the average GF vanishes. The self-averaging property of the NCF therefore seems to be in contradiction with the deterministic approach that claims that the NCF is equal to the exact Green's function when the diffuse field is equipartitioned.
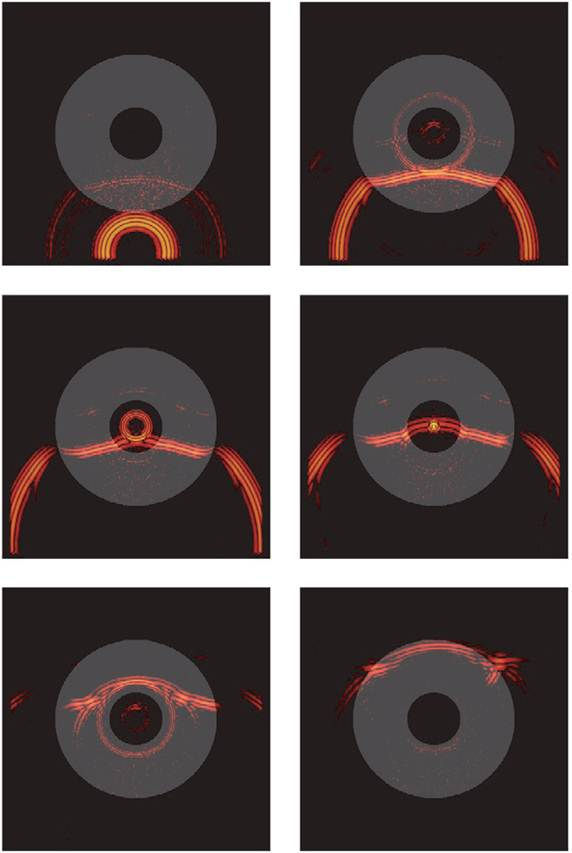
In this article, we derive the average and the variance of the cross-correlation of a noise wavefield. We first explain from the ladder approximation how the diffusion halo plays the role of secondary sources to reconstruct the mean Green’s function. We show that the last scattering events around the receivers play the role of secondary sources and help improving the estimation of the average GF. This is clearly observed on the following figure in which a halo with a skin depth of about one mean free path around the receivers located in the middle of the figure appears.
We also explicitly estimate the variance of the NCF which the key parameter for any practical application. The variance is derived using advanced multiple scattering theory and is linked with long-range correlations that appear in multiple scattering media. An infinite-range correlation term dominates fluctuations of NCF. Whereas the variance of a self-averaging estimator should ideally vanish when the number of sources and/or the observation time increases, this non-vanishing term proves that NCF is not a self-averaging quantity with respect to the plurality of noise sources. Numerical simulations confirm our theoretical investigations.
Those fundamental results can be applied to many different fields such as seismology, acoustics, microwave, optics or material science. In acoustics and in seismology, the estimation of the NCF is easily performed by the direct cross-correlation of recorded time-dependent fields. However, the noise sources are usually not uniformly distributed and a generalization of our approach to more complex source distributions would be a probe of the convergence of the NCF towards the GF for a single realization of disorder. This issue is of importance for imaging purposes. In the other hand, in optics, one can take benefit of the thermal noise that is uniform at thermal equilibrium. But then it is more tedious to measure the NCF. These results are also of importance in material science, metallic nanostructures can for instance be excited with surface plasmons in disordered media. Measuring the NCF at thermal equilibrium would make possible to estimate the CDOS.
de Rosny, J. & Davy, M. Green's function retrieval and fluctuations of cross density of states in multiple-scattering media. EPL (Europhysics Letters) 106, 54004 (2014).

Commentaires